GNN(Graph Neural Network)圖像化神經網路part1._柯尼斯堡七橋問題(Seven Bridges Problem)
Neural networks have been adapted to leverage the structure and properties of graphs.
We explore the components needed for building a graph neural network - and motivate the design choices behind them.
上圖比較關鍵的思想在於每個節點來自於上一層哪些節點計算而來。
GNN透過在每一層中將節點的表示更新為其鄰居節點的加權和，然後將這些更新後的表示作為下一層的輸入，從而逐漸地融合局部和全局信息，並在最終的表示中捕獲圖的結構和特徵。
GNN（Graph Neural Network）圖神經網路
- 「圖」是由節點（Node）與邊（Edge）所構成的資料結構
- GNN 是將圖結構引入深度學習中的神經網路，可以幫助我們分析複雜資料之間的關聯，像是社群關係、交通網路或推薦系統等等。
- GNN 可被視為是 CNN 的泛化版本。
- 世界上有許多資料是以圖的形式表示的
知識圖譜(智能客服)
一個人可能有多重身分是誰的妻子or丈夫，或也同時是哪間公司的高管之類的
道路交通動態流量預測
圖神經網路發表相關研究文獻逐漸攀升
Neural Networks extended by GNNs
柯尼斯堡七橋問題(Seven Bridges Problem)
圖論中的著名問題，當時東普魯士柯尼斯堡(Königsberg)也是今日俄羅斯加里寧格勒，市區跨普列戈利亞河兩岸，河中心有兩個小島。小島與河的兩岸有七條橋連接。
當時附近小鎮的鎮長一位數學家卡羅·戈特利布·依勒(Carl Gottlieb Ehler)
吃飽太閒就好奇以下問題:
哪一條路徑可以讓人穿越這七座橋，並且同一座橋只能經過一次。
其實更白話來說就是一筆畫問題。
1736年，當年29歲的數學家尤拉收到卡羅的信求助這一到難題，證明了七橋問題是無解的。
並在當時提出了所謂「位置幾何學」也就是現今「圖論」。歐拉將柯尼斯堡的實際情況抽像成了二維空間上點與線的組合，橋可以視為線（邊），橋連接的陸地視為點（頂點）。
有兩座已經在二戰時的大轟炸中被損毀，另外兩座則被改建成快速公路。其餘三座則原址保留，當中又有一座於1935年被重建。
當時的七座橋，至今剩下五座，令奇頂點只剩下兩個，所以可以一次過走完五座橋。
圖的組成
圖由很多個點(Vertex / node)、邊(Edge)組成
點(Vertex / node)
點根據不同應用可以由不同，應用於狼人殺遊戲中，每一個點就代表人。
點由一個特徵向量來表示。
邊(Edge)
又分有向無向
若在人際網路中又代表互相是否認識，此外邊也可用特徵向量去表示。
基本上又分為有向圖和無向圖，有時候可能在不同情境有不一樣解釋含意。
- 比方我主動去追蹤你IG但你不見得也有追蹤我這個誰追蹤誰有方向性
- 飛機航班起迄也是有方向性。
- 文章引用關係，A文章去引用B文章(出現比較早)這個也算是有向邊。
描述整個圖的通用屬性，比方化合物的總體性質或社交網絡的類型。
在某些模型中，可能會存在一個稱之為主節點（master node）的特殊節點來代表整個圖。
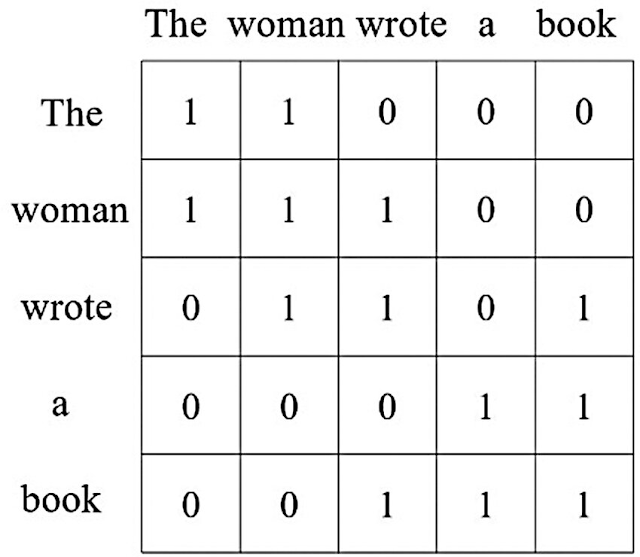
鄰接矩陣(adjacency matrix)
圖可透過「(鄰接)矩陣」來表示
事件萬物非規則性的數據事實上都能用圖的鄰接矩陣來表示
比方一句話中各個單詞，前後主格、受格、詞性之間關係，過往也有相關研究這麼設計。
https://www.researchgate.net/publication/364218631_A_text_classification_method_based_on_LSTM_and_graph_attention_network
GNN用於解決的問題類型
Node-level Task
旨在預測圖形輸入中節點的某些屬性。
預測可以是離散的類標籤，即節點分類，也可以是連續量，即節點回歸。
預測可以是離散的類標籤，即節點分類，也可以是連續量，即節點回歸。
Edge-level Task
旨在預測每個節點的屬性，而邊緣級任務側重於預測兩個節點之間是否存在邊或預測與圖形輸入上的邊關聯的某些屬性。
邊緣級任務通常稱為鏈路預測(Link prediction)問題。
邊緣級任務通常稱為鏈路預測(Link prediction)問題。
Graph-level Task
圖形級任務將輸入圖形視為一個整體，旨在預測其屬性。
如果要預測的屬性是離散的類標籤，我們將此任務稱為圖分類任務。
如果它旨在預測圖的連續屬性，則稱為圖回歸任務。
Ref:
A review of graph neural networks: concepts, architectures, techniques, challenges, datasets, applications, and future directions
Graph neural networks: A review of methods and applications
Graph Neural Networks: Graph Classification (Part III)
無所不在的圖神經網路任務，手把手教你簡單預測A跟E是不是朋友？
圖像化神經網路(1)：Graph Neural Network小簡介
留言
張貼留言