LeetCode資料結構_二分搜索(Binary Search)

-
 通常假設搜尋對象是一個有序的數列。這種搜尋算法通過將數列分成兩半，並比較中間元素與目標值的大小來迅速定位目標值的位置。

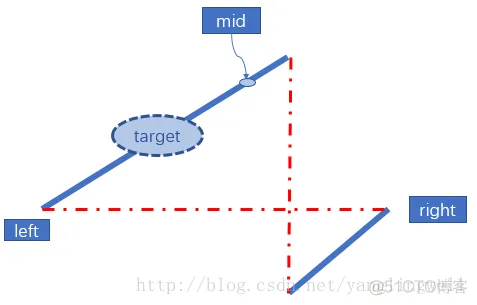
固定左右邊界，用中間值與目標值判斷大小，根據情況收縮左邊界或者右邊界即可。




https://ninagirl1998.medium.com/leetcode-33-search-in-rotated-sorted-array-da1df6111576


https://www.guru99.com/binary-search.html


假設我們有一個有序的整數陣列：[2, 5, 8, 12, 16, 23, 38, 45, 56, 72, 91]，現在我們想要找到目標值 23 是否在這個陣列中，如果在，我們還希望知道它的索引位置。

傳統的線性搜索方法是從陣列的第一個元素開始，逐一比較直到找到目標值或者確定目標值不存在。但是這種方法的時間複雜度是O(n)，當數列很大時，效率較低。

運用二分搜索的方法
Step1.
首先指定搜索範圍，即整個數列。左邊界設置為0，右邊界設置為陣列長度減1：left = 0，right = 10（假設陣列索引從0開始計算）。

Step2.
接下來，我們計算中間元素的索引：mid = (left + right) / 2 = 5。

Step3.比較中間元素23與目標值23的大小。[2, 5, 8, 12, 16, 23, 38, 45, 56, 72, 91]
由於它們相等，我們已經找到目標值，並且其索引為5。

Step4.搜索結束。


透過二分搜索，我們只用了幾次比較就找到了目標值的位置。這種方法的時間複雜度是O(log n)，比線性搜索的O(n) 效率更高。當數列很大時，二分搜索的優勢就會體現出來。


在有序數列中，二分搜索的平均時間複雜度是O(log n)，非常高效。特別在大數據量下，相比於線性搜索的O(n)，速度快得多。


二分搜索是一種高效的搜尋算法，特別適用於有序數列。它通過將搜索範圍分為兩半來迅速定位目標值，從而大大節省了搜索的時間。


69. Sqrt(x)(Easy)
https://leetcode.com/problems/sqrtx/
題目描述：計算非負整數 x 的平方根。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include <iostream>

int mySqrt(int x) {
    if (x <= 1) return x; // 當 x 為 0 或 1 時，直接返回 x

    int left = 1;
    int right = x;

    while (left <= right) {
        int mid = left + (right - left) / 2;
        int sqrtVal = x / mid;

        if (sqrtVal == mid) {
            return mid;
        } else if (sqrtVal < mid) {
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }

    return right; // 因為最後一次 mid * mid 小於 x，返回 right 即可
}

int main() {
    int x = 8;
    int result = mySqrt(x);
    std::cout << "Sqrt(" << x << ") = " << result << std::endl;
    return 0;
}

Step1.處理特殊情況：如果 x 為 0 或 1，則直接返回 x，因為它們的平方根就是它們自己。

Step2.定義兩個變數 left 和 right，分別表示搜索的範圍。
初始時，left 設置為 1（因為平方根不會大於 x 的一半），right 設置為 x。

Step3.進入 while 迴圈，條件是 left <= right，當 left 大於 right 時，搜索範圍內沒有找到平方根，就退出迴圈。

Step4.在迴圈內部，計算中間點 mid，mid 等於 left 和 right 的平均值。

Step5.計算 mid 的平方根值 sqrtVal，即 sqrtVal = x / mid。

Step6.進行判斷:
如果 sqrtVal 等於 mid，則 mid 就是 x 的平方根，直接返回 mid。
如果 sqrtVal 小於 mid，則 x 的平方根在 mid 的左半部分，所以將 right 更新為 mid - 1。
如果 sqrtVal 大於 mid，則 x 的平方根在 mid 的右半部分，所以將 left 更新為 mid + 1。

Step7.重複執行步驟3到步驟6，直到找到平方根或搜索範圍內沒有找到平方根。

Step8.在 while 迴圈結束後，返回 right 的值，因為最後一次 mid * mid 小於 x，而 right 正好是小於平方根的整數值，所以返回 right 即可。

測試案例 1:
int x = 4;
int result = mySqrt(x);
// 4 的平方根為 2
// 預期輸出: 2
測試案例 2:
int x = 8;
int result = mySqrt(x);
// 8 的平方根取整為 2，因為 2 * 2 = 4 < 8 且 3 * 3 = 9 > 8
// 預期輸出: 2
測試案例 3:
int x = 16;
int result = mySqrt(x);
// 16 的平方根為 4
// 預期輸出: 4
測試案例 4:
int x = 25;
int result = mySqrt(x);
// 25 的平方根為 5
// 預期輸出: 5
測試案例 5:



35. Search Insert Position(Easy)
https://leetcode.com/problems/search-insert-position/
給定一個排序的整數陣列和一個目標值 target，如果目標值存在於數列中，則返回其索引；如果不存在，則返回它應該被插入的位置索引，使得數列仍然保持有序。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>
#include <vector>

int searchInsert(std::vector<int>& nums, int target) {
    int left = 0;
    int right = nums.size() - 1;

    while (left <= right) {
        int mid = left + (right - left) / 2;

        if (nums[mid] == target) {
            return mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }

    return left; // 因為最後一次 left 越過 target 的位置，所以返回 left 即可
}

int main() {
    std::vector<int> nums = {1, 3, 5, 6};
    int target = 5;
    int result = searchInsert(nums, target);
    std::cout << "Target " << target << " should be inserted at index: " << result << std::endl;
    return 0;
}

Step1.定義函式 int searchInsert(vector<int>& nums, int target)，輸入一個排序的整數陣列 nums 和目標值 target，返回目標值在陣列中的索引或應該插入的位置索引。

Step2.定義兩個變數 left 和 right，分別表示搜索的範圍。初始時，left 設置為 0，right 設置為陣列長度減1。

Step3.進入 while 迴圈，條件是 left <= right，當 left 大於 right 時，搜索範圍內沒有找到目標值，就退出迴圈。

Step4.在迴圈內部，計算中間點 mid，mid 等於 left 和 right 的平均值。

Step5.進行判斷
如果 nums[mid] 等於 target，則表示目標值已經存在於陣列中，直接返回 mid。
如果 nums[mid] 小於 target，則目標值在 mid 的右半部分，所以將 left 更新為 mid + 1。
如果 nums[mid] 大於 target，則目標值在 mid 的左半部分，所以將 right 更新為 mid - 1。

Step6.重複執行步驟 3 到步驟 5，直到找到目標值或搜索範圍內沒有找到目標值。

Step7.在 while 迴圈結束後，返回 left 的值，因為最後一次 left 越過了目標值的位置，所以返回 left 即可，這也是應該插入的位置索引。
測試案例 1:
std::vector<int> nums = {1, 3, 5, 6};
int target = 5;
int result = searchInsert(nums, target);
// 由於 5 已經存在於陣列中，它的索引應該為 2
// 預期輸出: 2
測試案例 2:
std::vector<int> nums = {1, 3, 5, 6};
int target = 2;
int result = searchInsert(nums, target);
// 2 不存在於陣列中，但它應該插入在索引 1 的位置，即在 3 的前面
// 預期輸出: 1
測試案例 3:
std::vector<int> nums = {1, 3, 5, 6};
int target = 7;
int result = searchInsert(nums, target);
// 7 不存在於陣列中，但它應該插入在索引 4 的位置，即在 6 的後面
// 預期輸出: 4
測試案例 4:
std::vector<int> nums = {1, 3, 5, 6};
int target = 0;
int result = searchInsert(nums, target);
// 0 不存在於陣列中，且它比陣列中的最小值 1 還要小，應該插入在索引 0 的位置
// 預期輸出: 0
測試案例 5:
std::vector<int> nums = {1, 3, 5, 6};
int target = 8;
int result = searchInsert(nums, target);
// 8 不存在於陣列中，且它比陣列中的最大值 6 還要大，應該插入在索引 4 的位置
// 預期輸出: 4

704. Binary Search(Easy)
https://leetcode.com/problems/binary-search/
給定一個排序的整數陣列和目標值，使用二分搜索找到目標值在陣列中的索引，如果不存在，則返回-1。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>
#include <vector>

int search(std::vector<int>& nums, int target) {
    int left = 0;
    int right = nums.size() - 1;

    while (left <= right) {
        int mid = left + (right - left) / 2;

        if (nums[mid] == target) {
            return mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }

    return -1;
}

int main() {
    std::vector<int> nums = {-1, 0, 3, 5, 9, 12};
    int target = 9;
    int result = search(nums, target);
    std::cout << "Target " << target << " found at index: " << result << std::endl;
    return 0;
}

Step1.定義函式 int search(vector<int>& nums, int target)，輸入一個排序的整數陣列 nums 和目標值 target，返回目標值在陣列中的索引或-1（表示目標值不存在）。

Step2.定義兩個變數 left 和 right，分別表示搜索的範圍。初始時，left 設置為 0，right 設置為陣列長度減1。

Step3.進入 while 迴圈，條件是 left <= right，當 left 大於 right 時，搜索範圍內沒有找到目標值，就退出迴圈。

Step4.在迴圈內部，計算中間點 mid，mid 等於 left 和 right 的平均值。

Step5.進行判斷：
如果 nums[mid] 等於 target，則表示目標值已經存在於陣列中，直接返回 mid。
如果 nums[mid] 小於 target，則目標值在 mid 的右半部分，所以將 left 更新為 mid + 1。
如果 nums[mid] 大於 target，則目標值在 mid 的左半部分，所以將 right 更新為 mid - 1。

重複執行步驟 3 到步驟 5，直到找到目標值或搜索範圍內沒有找到目標值。

在 while 迴圈結束後，返回 -1，表示目標值不存在於陣列中。

測試案例 1:
std::vector<int> nums = {-1, 0, 3, 5, 9, 12};
int target = 9;
int result = search(nums, target);
// 9 存在於陣列中，它的索引應該為 4
// 預期輸出: 4

測試案例 2:
std::vector<int> nums = {-1, 0, 3, 5, 9, 12};
int target = 2;
int result = search(nums, target);
// 2 不存在於陣列中，返回 -1
// 預期輸出: -1

測試案例 3:
std::vector<int> nums = {1, 2, 3, 4, 5};
int target = 3;
int result = search(nums, target);
// 3 存在於陣列中，它的索引應該為 2
// 預期輸出: 2

測試案例 4:
std::vector<int> nums = {1, 2, 3, 4, 5};
int target = 6;
int result = search(nums, target);
// 6 不存在於陣列中，返回 -1
// 預期輸出: -1

測試案例 5:
std::vector<int> nums = {};
int target = 5;
int result = search(nums, target);
// 空陣列中找不到任何元素，返回 -1
// 預期輸出: -1

測試案例 6:
std::vector<int> nums = {1};
int target = 1;
int result = search(nums, target);
// 唯一的元素為 1，它的索引應該為 0
// 預期輸出: 0




33. Search in Rotated Sorted Array (Medium)
https://leetcode.com/problems/search-in-rotated-sorted-array/
給定一個旋轉過的排序整數陣列，和一個目標值，搜索目標值並返回索引，如果不存在，則返回-1。(指的是原本是升序排序的整數陣列，在某個未知的旋轉點上進行了旋轉操作。這種情況下，陣列的前部分一部分會被移動到陣列的尾部，而陣列的尾部一部分會被移動到陣列的前部，這樣就產生了旋轉效果。)
例如，原本的升序排序陣列為：[0, 1, 2, 4, 5, 6, 7]，假設在索引2的位置進行了旋轉，將陣列前面的元素移到了尾部，得到旋轉過的排序整數陣列：[2, 4, 5, 6, 7, 0, 1]。
[0, 1, 2, 4, 5, 6, 7] -> [0,1] [2,4,5,6,7] -> [2,4,5,6,7] [0,1] -> [2, 4, 5, 6, 7, 0, 1]



假設已排序的Array在您事先未知的某個樞軸處旋轉。將獲得一個要搜索的目標值。如果在數組中找到則返回其索引，否則返回-1。

需要在這種旋轉過的排序整數陣列中進行二分搜索來尋找目標值。因為陣列中可能存在旋轉，所以不能直接應用經典的二分搜索，我們需要通過比較旋轉點前後的元素來確定適當的搜索方向。

Array向左或者向右最多移動array.size()/2次。
如果nums[middle] >= nums[l]，說明Array向左旋轉,否則Array向右旋轉。



在區間​​[left, right)​​​ 求的中間項​​mid = (left + right)
Case1.如果​​nums[left] <= target < mid​​​ 則​​target​​​ 在區間​​[left, mid)​
Case2.否則, ​​target​​​ 在區間​​[mid+1, right)​​ 內，在右邊的上升區間。






Step1.定義函式 int search(vector<int>& nums, int target)，輸入一個旋轉過的排序整數陣列 nums 和目標值 target，返回目標值在陣列中的索引或-1（表示目標值不存在）。

Step2.定義兩個變數 left 和 right，分別表示搜索的範圍。初始時，left 設置為 0，right 設置為陣列長度減1。

Step3.進入 while 迴圈，條件是 left <= right，當 left 大於 right 時，搜索範圍內沒有找到目標值，就退出迴圈。

Step4.在迴圈內部，計算中間點 mid，mid 等於 left 和 right 的平均值。

Step5.進行判斷
如果 nums[mid] 等於 target，則表示目標值已經存在於陣列中，直接返回 mid。

如果 nums[mid] 小於 nums[right]，則表示 mid 到 right 區間是有序的。此時，我們可以判斷 target 是否在此區間中，如果是，將 left 更新為 mid + 1；如果不是，將 right 更新為 mid - 1。

如果 nums[mid] 大於 nums[right]，則表示 left 到 mid 區間是有序的。此時，我們可以判斷 target 是否在此區間中，如果是，將 right 更新為 mid - 1；如果不是，將 left 更新為 mid + 1。


重複執行步驟 3 到步驟 5，直到找到目標值或搜索範圍內沒有找到目標值。

Step6.迴圈結束後，返回 -1，表示目標值不存在於陣列中。


33.程式碼

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <iostream>
#include <vector>

int search(std::vector<int>& nums, int target) {
    int left = 0;
    int right = nums.size() - 1;

    while (left <= right) {
        int mid = left + (right - left) / 2;

        if (nums[mid] == target) {
            return mid;
        } else if (nums[mid] < nums[right]) {
            if (nums[mid] < target && target <= nums[right]) {
                left = mid + 1;
            } else {
                right = mid - 1;
            }
        } else {
            if (nums[left] <= target && target < nums[mid]) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        }
    }

    return -1;
}

int main() {
    std::vector<int> nums = {4, 5, 6, 7, 0, 1, 2};
    int target = 0;
    int result = search(nums, target);
    std::cout << "Target " << target << " found at index: " << result << std::endl;
    return 0;
}

測試案例 1:
std::vector<int> nums = {4, 5, 6, 7, 0, 1, 2};
int target = 0;
int result = search(nums, target);
// 目標值0存在於旋轉過的排序整數陣列中，它的索引應該為4
// 預期輸出: 4

測試案例 2:
std::vector<int> nums = {4, 5, 6, 7, 0, 1, 2};
int target = 3;
int result = search(nums, target);
// 目標值3不存在於旋轉過的排序整數陣列中，返回-1
// 預期輸出: -1

測試案例 3:
std::vector<int> nums = {1};
int target = 0;
int result = search(nums, target);
// 目標值0不存在於旋轉過的排序整數陣列中，返回-1
// 預期輸出: -1

測試案例 4:
std::vector<int> nums = {3, 1};
int target = 1;
int result = search(nums, target);
// 目標值1存在於旋轉過的排序整數陣列中，它的索引應該為1
// 預期輸出: 1

測試案例 5:
std::vector<int> nums = {5, 1, 3};
int target = 3;
int result = search(nums, target);
// 目標值3存在於旋轉過的排序整數陣列中，它的索引應該為2
// 預期輸出: 2

測試案例 6:
std::vector<int> nums = {4, 5, 6, 7, 8, 1, 2, 3};
int target = 8;
int result = search(nums, target);
// 目標值8存在於旋轉過的排序整數陣列中，它的索引應該為4
// 預期輸出: 4

測試案例 7:
std::vector<int> nums = {4, 5, 6, 7, 8, 1, 2, 3};
int target = 9;
int result = search(nums, target);
// 目標值9不存在於旋轉過的排序整數陣列中，返回-1
// 預期輸出: -1


34. Find First and Last Position of Element in Sorted Array
https://leetcode.com/problems/find-first-and-last-position-of-element-in-sorted-array/
給定一個已排序的整數陣列和一個目標值，使用二分搜索找到目標值在陣列中的第一個和最後一個出現的位置。如果目標值不存在於陣列中，則返回 [-1, -1]。


需要進行兩次二分搜索來找到目標值在排序整數陣列中的第一次和最後一次出現的位置
在進行二分搜索時，要根據目標值和中間元素的大小關係來更新搜索範圍，並在找到目標值時繼續向左或向右搜索。

要注意處理邊界情況。例如，當目標值小於整個陣列的最小元素或大於整個陣列的最大元素時，搜索範圍將越界，這時要特別處理這些情況。


首先就是找最左側的下標，利用二分查找首先是找到有一個值是與目標值target是相等的，然後因為是找最左側的下標，所以把right=mid-1來一直往左邊去逼近最左側的值
至於找最右側的下標就是，將left=mid+1,來去逼近最右側的下標

34.程式碼

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <iostream>
#include <vector>

std::vector<int> searchRange(std::vector<int>& nums, int target) {
    int left = 0;
    int right = nums.size() - 1;
    int first = -1;
    int last = -1;

    // 尋找第一次出現的位置
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            first = mid;
            right = mid - 1; // 向左搜索
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }

    left = 0;
    right = nums.size() - 1;

    // 尋找最後一次出現的位置
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            last = mid;
            left = mid + 1; // 向右搜索
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else {
            right = mid - 1;
        }
    }

    return {first, last};
}

int main() {
    std::vector<int> nums = {5, 7, 7, 8, 8, 10};
    int target = 8;
    std::vector<int> result = searchRange(nums, target);
    std::cout << "Range of target " << target << " is [" << result[0] << ", " << result[1] << "]" << std::endl;
    return 0;
}


Step1.定義函式 std::vector<int> searchRange(std::vector<int>& nums, int target)，輸入一個已排序的整數陣列 nums 和目標值 target，返回包含目標值第一次和最後一次出現的索引的陣列，如果目標值不存在於陣列中，返回 [-1, -1]。


Step2.定義兩個變數 left 和 right，分別表示搜索的範圍。初始時，left 設置為 0，right 設置為陣列長度減1。


Step3.進入第一個 while 迴圈，條件是 left <= right，當 left 大於 right 時，搜索範圍內沒有找到目標值，就退出迴圈。

Step4.在第一個 while 迴圈內部，計算中間點 mid，mid 等於 left 和 right 的平均值。


Step5.進行判斷
如果 nums[mid] 等於 target，則表示找到目標值，但這不一定是第一次出現的位置。
我們需要向左搜索，將 right 更新為 mid - 1，繼續在左半部分尋找第一次出現的位置。
如果 nums[mid] 小於 target，則目標值在 mid 的右半部分，所以將 left 更新為 mid + 1。
如果 nums[mid] 大於 target，則目標值在 mid 的左半部分，所以將 right 更新為 mid - 1。

Step6.重複執行步驟 3 到步驟 5，直到找到目標值或搜索範圍內沒有找到目標值。

Step7.在第一個 while 迴圈結束後，如果找到目標值，則 left 為第一次出現的位置；如果未找到目標值，則返回 [-1, -1]。

Step8.定義一個變數 start，初始化為 left，表示第一次出現的位置。

Step9.進入第二個 while 迴圈，條件是 start <= right，當 start 大於 right 時，表示已經搜索完整個範圍，退出迴圈。


Step10.在第二個 while 迴圈內部，計算中間點 mid，mid 等於 start 和 right 的平均值。

Step11.進行判斷
如果 nums[mid] 等於 target，則表示找到目標值，但這不一定是最後一次出現的位置。
我們需要向右搜索，將 start 更新為 mid + 1，繼續在右半部分尋找最後一次出現的位置。
如果 nums[mid] 小於 target，則目標值在 mid 的右半部分，所以將 start 更新為 mid + 1。
如果 nums[mid] 大於 target，則目標值在 mid 的左半部分，所以將 right 更新為 mid - 1。

Step12.重複執行步驟 9 到步驟 11，直到找到目標值或搜索範圍內沒有找到目標值。

Step13.在第二個 while 迴圈結束後，如果找到目標值，則 right 為最後一次出現的位置；如果未找到目標值，則返回 [-1, -1]。

Step14.返回一個陣列，包含第一次和最後一次出現的位置 [left, right]。


Ref:
https://algo.monster/problems/binary_search_intro
https://studyalgorithms.com/array/search-rotated-sorted-array/
https://www.doabledanny.com/binary-search-javascript
https://leetcode.xiaotaoguo.com/p/leetcode-33/#%E8%A7%A3%E9%A2%98%E6%80%9D%E8%B7%AF
https://blog.csdn.net/sjt19910311/article/details/46412523
https://foolishhungry.com/find-first-and-last-position-of-element-in-sorted-array/
https://cloud.tencent.com/developer/article/1506692
https://leetcode.wang/leetCode-33-Search-in-Rotated-Sorted-Array.html

留言

張貼留言

這個網誌中的熱門文章

何謂淨重(Net Weight)、皮重(Tare Weight)與毛重(Gross Weight)

-
圖片
當談到貨物的重量時，往往會分成所謂的淨重(Net Weight)與毛重(Gross Weight)。 會有以下公式關係存在 淨重=毛重-皮重(包裝物的重量) 毛重=淨重+皮重 淨重( Net Weight 縮寫為N.W.) 指物品本身的重量，不包括容器或包裝材料的重量。 凈重是國際貿易中最常見的計重辦法。 例如，如果運輸原材料，原材料的重量就是所運輸貨物的淨重。包裝原材料的容器或包裝不計入淨重。同樣地，當我們考慮一罐豆子時，罐子內所含物品的重量就算作淨重。因此，淨重將包括豆子、罐頭里的任何液體，以及保存豆子所含的物品。 大多數 以重量為計價的貨物買賣 ，採用此計價方法。 若合同中並未明確規範以何種方式計量和計價時，按慣例以凈重計價。 毛重( Gross Weight 縮寫G.W.) 貨物連同它的包裝的重量，是你托運的所有物品的總重量。 皮重(Tare Weight) 指商品外包裝材料的重量(即運輸包裝的重量)，不包括內包裝材料和襯墊物的重量。 比方一個空的貨櫃、容器、或任何包裝材料的重量。 Net Net Weight純淨重 (指從Net Weight中扣除內包裝後的重量) 進出口商品為了因應運輸及消費需求, 一般都有內包裝與外包裝。 一般在買賣合同與信用狀中,通常只要求於裝箱單上註明Gross Weight和Net Weight即可, 但有些L/C 要求 Net Net Weight,大多是海關徵收從量稅時的依據 運輸重量對於航運業或者航空運輸等各自都通用這些術語 為何特別在意重量? 主要就在於會影響像是傳輸安全乘載限制。 就運輸層面(不同方式的運輸) 航空運輸：對機長而言，毛重包括皮重、產品淨重以及飛機、燃料、乘客和機組人員的重量。 公路/鐵路運輸:對於火車車長而言，毛重包括產品淨重、皮重和運輸車輛的重量。 水路航運運輸：對船長而言，毛重就是淨重和皮重之和。 就公司ERP成本角度 成本一般都會採用 "淨重" 主要是因為若用毛重，可能會有輔材不可控因素存在 比方一個 5cm 固定塑膠件，今天用一個 10cm 紙箱測重，明天用一個 100cm 紙箱測重，那可能就容易導致ERP資料比較會失真。 就物流層面來探討 通常還會有一名詞即所謂「實際重量」(Actual Weight) 根據稱重(過磅)所得到的重量，實際重量分為實際毛重(Gross Weig
閱讀完整內容

Architecture(架構) 和 Framework(框架) 有何不同?_軟體設計前的事前規劃的藍圖概念

-
圖片
一個應用程式(軟體) 不管是  互動拍照 也好、 投影也好、車牌偵測... 舞台演唱會後方電視牆的互動應用程序、 粒子特效、3D或2D遊戲  等等 開發者通常都需要在一開始做規劃 ㄟ  假設我今天要寫 跟影像有關 可能需要偵測、可能需要提取前景、可能需要偵測圓形 之類的 我有  emgucv 、AForge.Net、 opencv 等等可以用 但是 假設我今天要做的應用程序是需要有視窗介面的~~ emgucv 跟 C# windows form 媒合性 就很高 而且直接在 visual studio 做開發 opencv 我可能還需要依賴 Qt 之類等等  framework 假設我今天是要寫一個 演唱會電視牆互動粒子特效 可能就會挑   openframeworks  、 processing 、kinect 來寫互動 Achitecture  --->全稱 :  Software Architecture   軟體架構 Achitecture   由好多 framework 組成 軟體架構（Software Architecture）是一種軟體在開發前的設計藍圖， 用來告訴軟體的結構，功能，介面，用法，與其他系統的構連以及資料交換等等規範， 但它並沒有叫你要用什麼方式實作， 因此軟體架構通常會產生文件，圖樣，原型以及規格等， 就是沒有可用的程式碼，因為那不是軟體架構應該有的東西， 就像蓋房子時是給你藍圖，而不是一幢蓋好的房子。 軟體框架（Framework):是一個已經成形的方法，而且有程式碼實體 （例如鋼構工法也是要有鋼材才能做），並且會告訴你要如何使用它 （即 Framework Documentation，MSDN Library 即為一最佳例子）
閱讀完整內容

(2021年度)駕訓學科筆試準備題庫歸納分析_法規是非題

-
圖片
  若是出現 「必須」、「必需」、「...必...」、「應由」、「應先」、「應...」 則很高機率是圈 是非通常只要是如下字眼 「不必」+動詞 、「不需」「不須」、「可不」、「可以不」、「可立即」 有出現或符合的都選叉 (X)1.違規記點又不登記在駕照上，所以可以 不必理會 而任意違反交通規則。 (X)2.發生重大交通事故，為迅速恢復交通，清除現場，可 不必等待 肇事處理機關之指示，即可進行。 (X)3.道路駕駛練習，行車前 不必實施 車輛安全檢查，因為那是駕駛教練的工作。 (X)4.開車前， 不必檢查 機件安全，但在行駛中要隨時注意儀錶功能顯示，確保行車安全。 (X)5.煞車油若經常低於"MIN"線，只要添加即可， 不必到修理廠檢修 。 (X)6.冷卻系統只要副水箱在滿水位，主水箱 不必檢查 也不會有問題。 (X)7.引擎冷卻水內含有防凍液或防銹劑，可 不必更換 。 (X)8.儀錶板上的「燃油油量錶」之指針高度，已經降低至「E」點，橘色的「低油料警示燈」點亮時， 不必急著加油 ，到達目的地後再行補充燃油即可。 (X)9.有安全氣囊裝備的汽車， 不必繫 安全帶。 (X)10.煞車時有異音，是正常的情況， 不必檢修 。 (X)11.汽車定期檢驗 不必檢驗 車輛故障標誌，所以隨車不一定要帶車輛故障標誌。 (X)12.開車時 不必理會 義交之指揮，一切以號誌為主。 (X)13.汽車經過隧道，因隧道內燈光明亮視線良好，為省電可 不必開亮 頭燈。 (X)14.駕駛人只求技術優良，對遵守交通規則 不必太重視 。 (X)15.在開車前， 不必檢查 機件，以免耽誤行車時間。 (X)16.遇幼童專用車、校車、身心障礙者用特製車或教練車， 不必禮讓 。 (X)17.行車 不必攜帶 隨車工具。 (X)18.行車起駛前進， 不必顯示 方向燈。 (X)19.汽車通過鐵路平交道，前後兩車間， 不必保持 距離。 (X)20.夜間將車輛停放在無燈光設備及照明不清之道路時，亦 不必顯示 停車燈光或反光標識。 (X)21.在夜間或有霧靄、雨雪、風沙及晝晦時，把車輛停在路旁， 不必顯示 停車燈光或反光標識。 (X)22.汽車駕駛人，僅需具有優良駕駛技術， 不需 具備急救的常識和技能。 (X)23.汽車車身、引擎、底盤、電系等重要設備變更或調換時， 不需 向公路主管機關申請臨時檢驗。
閱讀完整內容