機器學期常見到的統計學筆記_常見的統計量(Statistics)用來作為特徵表徵(Feature representation)

可以假設有兩個班級學生，哪個班級學生分數表現平均看起來會較好

A班

100,98,95,90,100,90

B班

80,65,72,77,79,80

你當然可以說直接看就是A班比較好但是在資料科學領域，主要探討資料背後隱含的特性以及挖掘更多有用的資訊。

在此可透過期望值更準確來去評比哪個班級的分數較好，期望成績會較高。

A班跟B班考試成績每一個同學都服從均勻分布，也就是權重都一樣。

A班的期望值： $\frac{100+98+95+90+100+90}{6}=\frac{573}{6}=95.5$

B班的期望值： $\frac{80+65+72+77+79+80}{6}=\frac{453}{6}=75.5$

所以，A班的平均成績是95.5，B班的平均成績是75.5。

在期望值估算下A班會來得比B班會考更好。

因此我們會需要注重有捨麼樣子的特性可拿來做有效的資訊利用

通常就會利用統計量(Statistics)  作為ML及資料科學中的特徵表徵(Feature representation)

四個常見的統計量如下

1.期望值(Expectation)

有時也會叫平均數(average)

主要就是希望在事情尚未發生時，透過過去蒐集到的資料中，進行統計推論得到一個預期出現的值。

設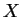為一離散型的隨機變數, 且可能取值為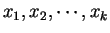, 則 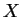之期望值定義為

換言之，期望值其實就是計算加權平均，權重就是P(x)。

其中表隨機變數取值在之機率值, 對。
換言之，設定隨機變數X的機率分布為P(x)，這個機率分布也可視為其權重。

例如, 投擲一公正的骰子, 也就是1,2,3,4,5,6每個面出現的機率皆為1/6, 令隨機變數表

所出現之點數, 則 =1/6,   , 因此之期望值為

            。

在一般公平認知的六面骰子中，權重都會固定是1/6，因此就會是我們一般認知的平均數。

標準常態分佈（也稱為標準正態分佈）是一種特殊的概率分佈，其機率密度函數（probability density function，簡稱PDF）是一個鐘形曲線，通常被稱為正態分佈曲線或鐘形曲線。標準常態分佈的平均值（期望值）是0，標準差為1。

這意味著如果你從標準常態分佈中抽取一個隨機變數，它的期望值（平均值）將等於0。具體來說，如果你從標準常態分佈中抽取大量的數據點，將這些數據點相加並求平均值，你將會得到一個接近0的值。

標準常態分佈的機率密度函數的公式如下：

$�(�)=\frac{1}{\sqrt{2�}}{�}^{-\frac{{�}^2}{2}}$

其中，$�$x 是隨機變數的值，$�$e 是自然對數的底數，$�$π 是圓周率。
這個公式描述了標準常態分佈的形狀，並告訴你在不同x值處的機率密度。

如果我們有一個一般的正態分佈（不一定是標準正態分佈，即平均值不為0，標準差不為1），我們可以使用z-score（z值）來標準化（將其轉換為標準正態分佈）。 z-score 是一個測量隨機變數在正態分佈中位置的標準化值。

z-score 的計算方式如下：

$�=\frac{�-�}{�}$

其中，

• $�$ 是 z-score。
• $�$ 是隨機變數的值。
• $�$ 是正態分佈的平均值。
• $�$ 是正態分佈的標準差。

將隨機變數的值減去平均值，然後除以標準差，這樣就可以將這個值轉換為以標準差為單位的標準正態分佈中的位置。如果 z-score 為正，則表示該值高於平均值；如果 z-score 為負，則表示該值低於平均值。 使用 z-score 的好處之一是可以將不同正態分佈之間的數據進行比較，因為它們都可以轉換為相同的標準正態分佈。

假設我們有一個正態分佈，平均值為 $�=50$，標準差為 $�=10$，我們想知道 x = 60 的 z-score：

$�=\frac{60-50}{10}=1$

這表示 x = 60 的值在這個正態分佈中的位置為平均值的一個標準差之上。 總之， z-score 是一種用於將一般正態分佈轉換為標準正態分佈的標準化方法

2.各階中心動差(moment)

用來評估隨機變數跟特定值a之間的差異n次方之期望值。

一般用的叫做中心(中央)動差,主動差(Central moment)，n階中心動差是關於數據分佈的更高階特徵，可以用於深入了解數據集的形狀和分佈，也就是以平均數μ為中心的n階動差。

n階中心動差： ${�}_{�}=\frac{1}{�}{\sum }_{�=1}^{�}({�}_{�}-\overline{�}{)}^{�}$

• n 是要計算的中心動差的階數。
• $�$ 是數據點的總數。
• ${�}_{�}$ 是第i個數據點的值。
• $\overline{�}$ 是數據集的平均值。

可以使用期望值的定義來計算這個中心動差。期望值（μ）的定義如下：

μ=N1​∑i=1N​xi​

使用期望值的定義來簡化中心動差的計算。首先，我們將 ${�}_{�}$ 重新寫成 $\overline{�}+({�}_{�}-\overline{�})$，然後展開n次方項：

$$\begin{array}{rl}{\displaystyle <span\; style="background-color:\; white;">(</span>{\mathrm{<span\; style="background-color:\; white;">�</span>}}_{\mathrm{<span\; style="background-color:\; white;">�</span>}}<span\; style="background-color:\; white;">-</span>\stackrel{<span\; style="background-color:\; white;">ˉ</span>}{\mathrm{<span\; style="background-color:\; white;">�</span>}}{<span\; style="background-color:\; white;">)</span>}^{\mathrm{<span\; style="background-color:\; white;">�</span>}}}& {\displaystyle <span\; style="background-color:\; white;">=</span><span\; style="background-color:\; white;">[</span><span\; style="background-color:\; white;">(</span>{\mathrm{<span\; style="background-color:\; white;">�</span>}}_{\mathrm{<span\; style="background-color:\; white;">�</span>}}<span\; style="background-color:\; white;">-</span>\stackrel{<span\; style="background-color:\; white;">ˉ</span>}{\mathrm{<span\; style="background-color:\; white;">�</span>}}<span\; style="background-color:\; white;">)</span><span\; style="background-color:\; white;">+</span>\stackrel{<span\; style="background-color:\; white;">ˉ</span>}{\mathrm{<span\; style="background-color:\; white;">�</span>}}{<span\; style="background-color:\; white;">]</span>}^{\mathrm{<span\; style="background-color:\; white;">�</span>}}}\\ {\displaystyle }& {\displaystyle <span\; style="background-color:\; white;">=</span>\underset{\mathrm{<span\; style="background-color:\; white;">�</span>}<span\; style="background-color:\; white;">=</span>\mathrm{<span\; style="background-color:\; white;">0</span>}}{\overset{\mathrm{<span\; style="background-color:\; white;">�</span>}}{<span\; style="background-color:\; white;">\sum </span>}}<span\; style="background-color:\; white;">(</span>\genfrac{}{}{0px}{}{\mathrm{<span\; style="background-color:\; white;">�</span>}}{\mathrm{<span\; style="background-color:\; white;">�</span>}}<span\; style="background-color:\; white;">)</span><span\; style="background-color:\; white;">(</span>\stackrel{<span\; style="background-color:\; white;">ˉ</span>}{\mathrm{<span\; style="background-color:\; white;">�</span>}}<span\; style="background-color:\; white;">-</span>{\mathrm{<span\; style="background-color:\; white;">�</span>}}_{\mathrm{<span\; style="background-color:\; white;">�</span>}}{<span\; style="background-color:\; white;">)</span>}^{\mathrm{<span\; style="background-color:\; white;">�</span>}}{\stackrel{<span\; style="background-color:\; white;">ˉ</span>}{\mathrm{<span\; style="background-color:\; white;">�</span>}}}^{\mathrm{<span\; style="background-color:\; white;">�</span>}<span\; style="background-color:\; white;">-</span>\mathrm{<span\; style="background-color:\; white;">�</span>}}}\end{array}$$

其中，$\left(\genfrac{}{}{0px}{}{�}{�}\right)$ 表示組合數，表示選擇k個項目的方式。 現在，可以將這個展開式代入中心動差的公式：

$$\begin{array}{rl}{\displaystyle {�}_{�}}& {\displaystyle =\frac{1}{�}\sum _{�=1}^{�}(\sum _{�=0}^{�}\left(\genfrac{}{}{0px}{}{�}{�}\right)(\overline{�}-{�}_{�}{)}^{�}{\overline{�}}^{�-�})}\\ {\displaystyle }& {\displaystyle =\sum _{�=0}^{�}\left(\genfrac{}{}{0px}{}{�}{�}\right){\overline{�}}^{�-�}\frac{1}{�}\sum _{�=1}^{�}(\overline{�}-{�}_{�}{)}^{�}}\end{array}$$

現在，我們可以觀察到 $\frac{1}{�}{\sum }_{�=1}^{�}(\overline{�}-{�}_{�}{)}^{�}$

$\frac{1}{�}{\sum }_{�=1}^{�}(\overline{�}-{�}_{�}{)}^{�}$ 就是n階中心動差 ${�}_{�}$，因為它衡量了數據點相對於平均值的k次方的平均值。所以，我們可以將公式簡化為：

μn​=k=0∑n​(kn​)xˉn−kμk​

公式描述了n階中心動差（${�}_{�}$）和較低階中心動差（${�}_{�}$，其中$�<�$）之間的關係。這樣，我們可以通過計算較低階的中心動差來獲得更高階的中心動差。

當 $�=0$ 時，我們要計算的是 0 階中心動差，即常數項。這是一個簡單的情況，因為所有的數據點都對平均值的偏移量均為0，因此它們的 0 次方也都是1。

當 $�=1$ 時，我們要計算的是 1 階中心動差，即數據點相對於平均值的偏移量的平均值。這就是平均絕對偏差（Mean Absolute Deviation，MAD）計算如下：

當 $�=2$ 時，我們要計算 2 階中心動差，這代表數據點相對於平均值的偏移量的平方的平均值，這就是方差（Variance）。計算如下：

2階中心動差表示數據點相對於平均值的偏離的平方的平均值，其數學表示為：

${�}_2=\frac{1}{�}{\sum }_{�=1}^{�}({�}_{�}-\overline{�}{)}^2$

方差（Variance）也是用來衡量數據集的變異性，其數學表示也為：

$\text{Var}(�)=\frac{1}{�}{\sum }_{�=1}^{�}({�}_{�}-�{)}^2$

其中，$�$ 是數據點的總數，${�}_{�}$ 是第i個數據點的值，$�$ 是數據集的期望值（平均值）。

需要注意的是，這兩個公式的結構非常相似，只是符號不同。實際上，它們描述的概念是相同的，都是衡量數據點相對於中心（平均值）的離散程度。

常見表示方式如下，是假設當X有n個樣本點，且服從均勻分布(每個出線機率都固定)。

Var(X)=N1​∑i=1N​(xi​−μ)2

=E[(X−μ)2]

當 $�=3$ 時，我們要計算 3 階中心動差，這代表數據點相對於平均值的偏移量的立方的平均值，通常用於計算偏度（Skewness）。計算如下：

「偏度」:量化隨機變數機率的不對稱性

https://academic-accelerator.com/encyclopedia/zh/skewness

當 $�=4$ 時，我們要計算的是 4 階中心動差（fourth central moment），它表示數據點相對於平均值的偏移量的四次方的平均值。其數學表示為：

${�}_4=\frac{1}{�}{\sum }_{�=1}^{�}({�}_{�}-\overline{�}{)}^4$

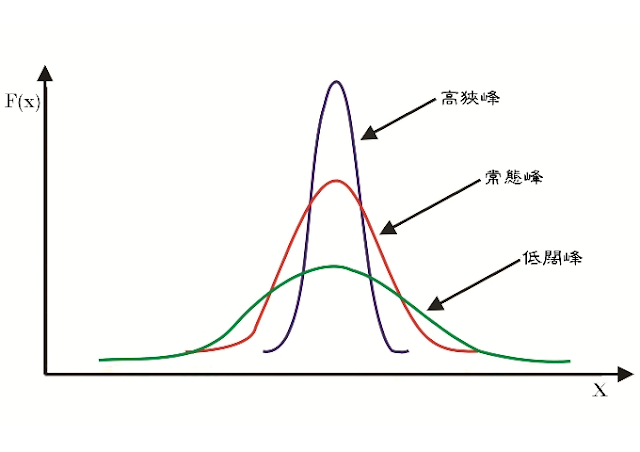
用於描述隨機變數的分布的峰度（kurtosis）

https://hackmd.io/@JiaYuan45147/rJv7zcsEI

一般來說，峰度是基於四次方的統計量，它的定義如下：

$\text{Kurtosis}=\frac{�[(�-�{)}^4]}{(�[(�-�{)}^2]{)}^2}$

其中，$�$ 是一個隨機變數，$�$ 是 $�$ 的期望值，$�$ 代表期望值運算符。

峰度有幾種不同的定義方式，最常見的定義是基於 Excess Kurtosis，即減去正態分布的峰度值3，這樣正態分布的峰度為0。

高峰度（正峰度）表示分布的峰值較高，尾部相對較重。低峰度（負峰度）表示分布的峰值較低，尾部相對較輕。一個正態分佈的峰度為0，因為它的峰值和尾部與標準正態分佈相同。

峰度的解釋取決於具體的應用，高峰度可能表示分布有更多的極端值或離群值，而低峰度可能表示分布較平穩。在某些統計應用中，峰度可以幫助我們了解數據的分佈特性，並且可以用來區分不同的分佈類型。

3.相關係數 和 共變異數

共變異數(Covariance) 可用來檢視多維度變數之間的相關性，是一個用來度量兩個隨機變數之間聯合變化程度的統計量。如果兩個變數一起增加或一起減少，共變異數是正數；如果一個變數增加而另一個減少，共變異數是負數；如果它們的變化趨勢無關聯，共變異數接近零。

Cov(X,Y)=E[(X−μX​)(Y−μY​)]

其中，$�$ 和 $�$ 是兩個隨機變數，${�}_{�}$ 和 ${�}_{�}$ 分別是它們的期望值。

相關係數(Correlation Coefficient) 依照共變異數得到的統計量。

Corr(X,Y)=σX​σY​Cov(X,Y)​

其中，$\text{Cov}(�,�)$ 是兩個隨機變數 $�$ 和 $�$ 的共變異數，${�}_{�}$ 和 ${�}_{�}$ 分別是它們的標準差。這個公式將共變異數標準化，使得它不會受到變數單位的影響，並且可以更容易地解釋變數之間的關係。

相關係數是共變異數的標準化版本，它的值範圍在 -1 到 1 之間。相關係數用於衡量兩個變數之間的線性關係的強度和方向。當相關係數接近 1 時，表示兩個變數之間存在強正線性關係；當相關係數接近 -1 時，表示存在強負線性關係；當相關係數接近 0 時，表示兩個變數之間幾乎沒有線性關係。

總結，共變異數測量它們的聯合變化，而相關係數衡量線性相關性的強度和方向。

4.共變異數矩陣(Covariance Matrix)

用來描述多維隨機變數之間協方差關係的重要工具。它是一個方陣，通常用於多元統計分析，可以提供關於多個變數之間的相關性和變異性的信息。

主要在於將隨機變數推廣到高維度。我們可以把多個變數排成行向量，組成一個矩陣，並且透過矩陣轉置、相乘來計算共變異數。

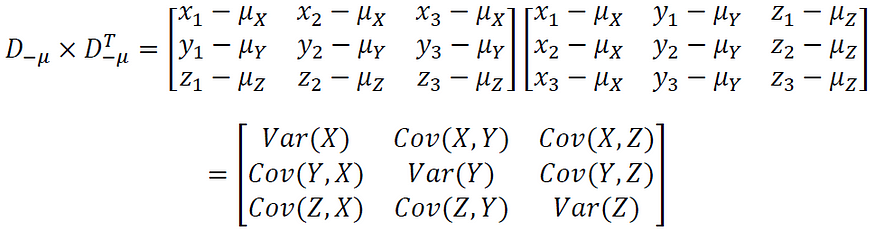
Ref:

https://www.stat.nuk.edu.tw/prost/content_new/c1-6.htm

https://flag-editors.medium.com/%E6%A9%9F%E5%99%A8%E5%AD%B8%E7%BF%92lesson-13-%E7%89%B9%E5%BE%B5%E5%B7%A5%E7%A8%8B%E4%B8%AD%E7%9A%84%E5%A5%87%E7%95%B0%E5%80%BC%E5%88%86%E8%A7%A3%E8%88%87%E5%85%B1%E8%AE%8A%E7%95%B0%E6%95%B8%E7%9A%84%E9%97%9C%E4%BF%82-21cf2b7a063a