資料探勘研究與實務_層次、階層式聚類/分層分群(Hierarchical Clustering)筆記_兩種聚類過程及兩種計算聚類間距離的方法

Clustering 聚類

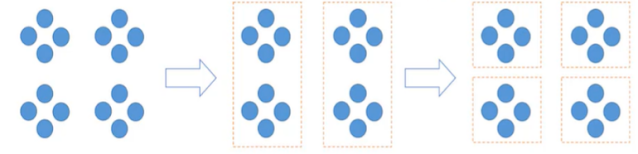
主要是探討某點群是要分2個聚類 還是4個 及如何劃分、劃分依據為何的過程。

分出來的聚類好壞評估十分主觀。

 

https://harshsharma1091996.medium.com/hierarchical-clustering-996745fe656b

在聚類/分群(Clustering)算法中其中一個叫做層次聚類(Hierarchical Clustering)

它藉由計算不同類別資料點之間的相似度來創建一棵有層次的嵌套聚類樹。

這個聚類樹中，不同類別的原始數據點位於數的最底層，樹的頂層則是一個聚類的樹根節點。

兩種聚類過程

層次聚類(Hierarchical Clustering)

有細分兩種聚類過程的策略分別是

1.自下而上合併(Agglomerative)

從將每個觀察值視為單獨的聚類開始，然後合併最接近的聚類，直到只有一個聚類為止。

在此會去計算點間距愈短代表離愈近也就是互相具備高相似性。

相似度計算基本上就會採用歐式距離Euclidean distance(兩點直線間距)做計算

步驟：

Step1.開始時，將每個數據點視為一個獨立的聚類，因此如果有 N 個數據點，就有 N 個聚類。

Step2.計算所有聚類間的距離。這通常使用歐幾里得距離，但也可以使用其他距離度量。

Step3.將距離最近的兩個聚類合併成一個新的聚類。

Step4.重新計算新的聚類與其他聚類之間的距離。

Step5.重複步驟3和4，直到所有數據點都被合併成一個聚類。

2.自上而下分裂(Divisive)

步驟：

Step1.開始時，所有的數據點都在一個大的聚類中。

Step2.選擇一個最大的聚類進行分裂。

Step3.使用某種方法（例如K-means聚類）來分裂聚類。

Step4.重複步驟2和3，直到每個數據點都被分裂成獨立的聚類。

基本上我們大多數時候都是針對Agglomerative做探討

兩種計算聚類間距離的方法(事實上不只這兩種)

對於如何決定哪兩個群集應該合併或如何分裂群集，我們可以使用以下方法:

(備註:另外還有其他方法Average Link , Ward...有空再補齊)

Single Link (最小連接法)

兩個聚類之間的距離是基於它們之間最近的兩個數據點的距離，最大程度地減少了成對的群集之間的距離。常用於較大數據集的層次聚類，因為可非常有效率進行計算。於非球形數據上表現也良好，但對帶雜訊的數據不夠穩健。

distance(A,B)=mina∈A,b∈B​d(a,b)

其中，$�$ 和 $�$ 是兩個聚類，而 $�(�,�)$ 是點 $�$ 和點 $�$ 之間的距離。

如果群集A中有點a和群集B中有點b，那麼群集A和群集B之間的距離就是所有a和b之間的距離中的最小值。

Complete Link (最大連接法)

兩個聚類之間的距離是基於它們之間最遠的兩個數據點的距，使成對的群集對之間的最大距離最小化。

distance(A,B)=maxa∈A,b∈B​d(a,b)

其中，$�$ 和 $�$ 是兩個聚類，而 $�(�,�)$ 是點 $�$ 和點 $�$ 之間的距離。

如果群集A中有點a和群集B中有點b，那麼群集A和群集B之間的距離就是所有a和b之間的距離中的最大值。

這些連接方法會影響到層次聚類的結果。例如，使用single link可能會導致更長和不均匀的聚類，而complete link則傾向於創建更緊密和均勻的聚類。

Agglomerative-Single Link

以下舉的例子是針對Agglomerative通過合併距離最近的兩個群集，逐步構建一個階層結構案例

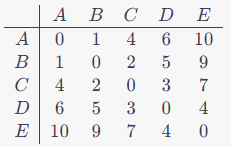
假設我們有五個點：A, B, C, D, E，其距離矩陣如下

例如點A到點B的距離為1，點C到點D的距離為3，等等。

使用單連接法進行階層式分群的步驟

開始時，每個點都被視為一個群集，所以我們有5個群集：{A}, {B}, {C}, {D}, {E}

Step1.查找距離矩陣中的最小值。最小值是1，位於A和B之間，所以我們合併A和B成一個群集。現在我們有4個群集：{A, B}, {C}, {D}, {E}。

Step2.更新距離矩陣，A,B合併然後其餘點距不變。新群集{A, B}到其他群集的距離是{A, B}中任何點到那些群集的最小距離。

例如，{A, B}到{C}的距離是A到C和B到C的距離中的最小值，即2。

在合併後，我們需要更新距離矩陣以反映新的群集結構。對於新群集{A,B}和任何其他群集（例如C），我們將距離定義為：

Distance({A,B},C)=min(Distance(A,C),Distance(B,C))

在我們的例子中，$\text{Distance}(�,�)=4$ 和 $\text{Distance}(�,�)=2$。因此，$\text{Distance}(\{�,�\},�)=\min (4,2)=2$。

重複步驟2和3，直到所有點都在同一群集中。

第1回合 (步驟2和3)

重複步驟2和3，直到所有點都在同一群集中。

第2回合 (步驟2和3)

合併群集:{A, B}, {C}

合併的距離: 2

結果的群集: {{A, B} , {C} }、D 跟 E

更新後的距離矩陣:

第三回合 (步驟2和3)

合併群集:{{A,B},C} 跟 D

合併的距離: 3

結果的群集: {{{A,B},C},D } 和 E

更新後的距離矩陣:

第四回合 (步驟2和3)

合併群集:{{{A,B},C},D } 和 E

合併的距離: 4

結果的群集: { {{{A,B},C},D } ,  E }

這時所有的點都被合併到一個群集中，所以不再有距離矩陣。

Agglomerative-Complete Link

在完整連接法中，兩個群集之間的距離定義為群集中最遠的兩個點之間的距離。這意味著，為了合併兩個群集，必須確保群集中的所有點都足夠接近。

這種方法的一個特點是它傾向於產生較為圓形或球形的群集，因為它考慮到了群集中的所有點，並確保了它們之間的最大距離。

以下舉的例子是針對Agglomerative通過合併距離最遠的兩個群集，逐步構建一個階層結構案例

假設我們有五個點：A, B, C, D, E，其距離矩陣如下

例如點A到點B的距離為1，點C到點D的距離為3，等等。

使用完整最大連接法進行階層式分群的步驟

開始時，每個點都被視為一個群集，所以我們有5個群集：{A}, {B}, {C}, {D}, {E}

Step1.找到最小距離：從距離矩陣中找到最小的距離。該距離表示兩個最接近的群集。

Step2.合併群集：合併距離最近的兩個群集成一個新的群集。

Step3.更新距離矩陣：刪除已合併群集的行和列，並添加新群集的行和列。新群集到其他群集的距離是使用完整連接法計算的，即新群集中的點和其他群集中的點之間的最大距離。

重複步驟1到3，直到所有數據點都合併到一個群集中，或直到達到所需的群集數。

第一回合:

在進行第一輪合併時，我們要找出距離最小的兩個群集。為了使用完整連接法確定群集之間的距離，我們需要考慮每個群集中所有點之間的最大距離。

但在這個階段，每個數據點都是一個獨立的群集，所以我們只需要考慮原始的距離矩陣。

從上述矩陣中，我們可以看到最小的非零距離是1，這是點A和點B之間的距離。

合併群集: A和B

合併的距離:1

結果的群集: {A,B} 、C、D 跟E

更新後的距離矩陣

在合併後，我們需要更新距離矩陣以反映新的群集結構。對於新群集{A,B}和任何其他群集

例如 C 

將距離定義為：

Distance({A,B},C)=max(Distance(A,C),Distance(B,C))

在我們的例子中，$\text{Distance}(�,�)=4$ 和 $\text{Distance}(�,�)=2$。因此，$\text{Distance}(\{�,�\},�)=\max (4,2)=4$。

這種方式保證了在新的群集

{A,B}和其他群集之間，考慮到了最遠的距離。

重複這個過程，我們可以為新群集和其他所有群集更新距離矩陣。

第二回合:

合併群集: {A,B} 和 C

合併的距離: 4

結果的群集:{{A,B},C}、D 和 E

更新後的距離矩陣:

第三回合:

合併群集: {{A,B},C} 和 D

合併的距離: 6

結果的群集: {{{A,B},C},D} 和 E

更新後的距離矩陣:

第四回合:

合併群集: {{{A,B},C},D} 和 E

合併的距離: 10

結果的群集: {{{{A,B},C},D},E}

這時所有的點都被合併到一個群集中，所以不再有距離矩陣。

每一回合都合併了距離最遠的兩個群集，直到所有的點都被合併到一個群集中。